Solution to the Jane Street Puzzle of February 2023: Twenty Four Seven (Four-in-One)
In this post, we will implement a backtracking algorithm to solve the Jane Street puzzle of February 2023. You can find the script containing all the code in this post in my GitHub.
Statement of the problem
Consider the following $12 \times 12$ grid, with four $7 \times 7$ subgrids:
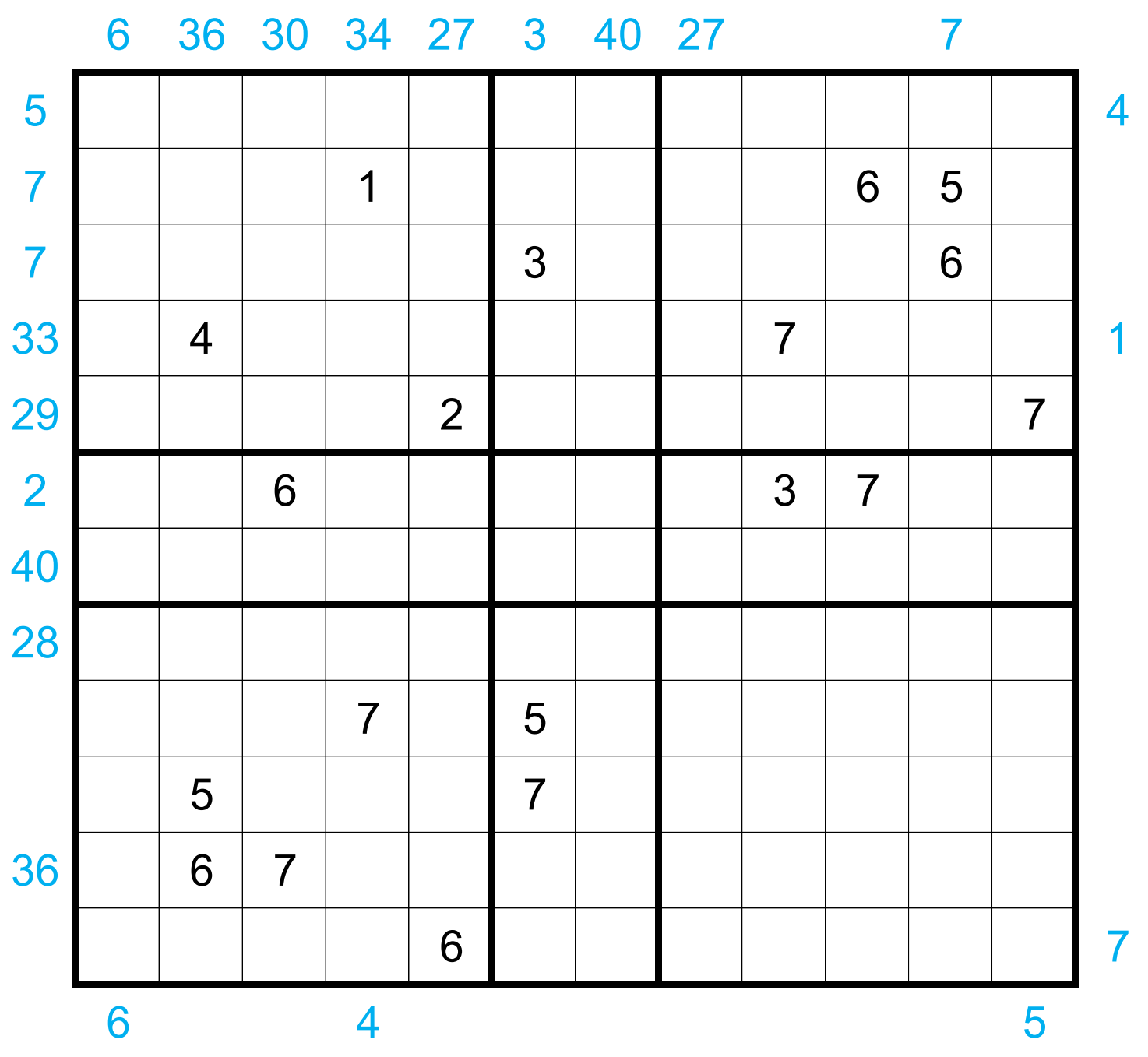
We want to fill each cell of the grid with a number in $\{0,\ldots,7\}$, such that the following constraints are satisfied:
- Each $7 \times 7$ subgrid has one $1$, two $2$’s, …, seven $7$’s.
- Each row/column in every $7 \times 7$ subgrid contains exactly four nonzero numbers. The sum of every such row/column is $20$.
- Every $2 \times 2$ square in the grid must have at least one cell with a $0$.
- If a row/column in the $12 \times 12$ grid is marked with a blue number, then either that number is the sum of the row/column, or the blue number is the first nonzero value seen in that row/column.
- The numbered cells form a connected region.
Question: in the completed grid, what is the product of the areas of the connected groups of squares with a $0$?
Strategy: use a backtracking algorithm
Backtracking roughly works as follows. We maintain a stack of partial candidate solutions to our problem (a partial candidate is just a partially filled board). At every iteration, we examine a partial candidate and check if at this point, the constraints are still satisfied.
- If the constraints are not satisfied, we abandon this candidate and proceed to the next iteration, where we examine a new candidate.
- If the constraints are satisfied, we fill an empty cell with the possible values that could be in that cell, and add all the partial candidates obtained in this way to the stack.
At every iteration, we should also check if the board is completely filled.
An algorithm like this will obviously be significantly faster than brute-force search, but we can still improve on this. For example, suppose that cells $(0, 0)$, $(0,1)$ and $(1, 0)$ have been filled with positive numbers. We know that by the $2 \times 2$ constraint, cell $(1,1)$ must be $0$. But the algorithm above is not able to conclude that immediately: it would need to expand the current grid with all the possible values for cell $(1,1)$, and reject each invalid grid individually to conclude that $0$ is the only number that can be in cell $(1, 1)$.
Taking this into account, we can improve the algorithm as follows. Denote by xm the matrix (list of lists) representing the current board, where we set xm[i][j] = -1 if cell $(i, j)$ is currently not known. We will consider a matrix cm, where cm[i][j] is a bitmask representing the list of numbers that possibly could be in xm[i][j]. For example, if cm[i][j] contains the value $(154)_{10} = (10011010)_2$, this means that the numbers that could be in xm[i][j] are $\{7,4,3,1\}$. We can implement a function prune which uses the constraints of the problem to rule out some possible choices in each cell.
We will write a Python implementation of this program. Since we will be dealing with bit computations, the following quantities will be helpful.
count is an array where count[n] is the number of $1$s in the binary representation of $n$:
count = [0 for _ in range(1 << 8)]
for n in range(1, 1 << 8):
count[n] = 1 + count[n & (n - 1)]value is an array where value[n] is the location of the first $1$ in the binary representation of $n$:
value = [-1 for _ in range(1 << 8)]
for n in range(1, 1 << 8):
value[n] = next(v for v in range(8) if n & (1 << v))We define types Board = list[list[int]] (so that xm is of type Board) and Choices = list[list[int]] (so that cm is of type Choices). We can define functions that convert between the two types.
def board(cm: Choices) -> Board:
''' Given matrix of choices, return matrix of values. '''
x = lambda c: value[c] if count[c] == 1 else -1
return [[x(cm[i][j]) for j in range(12)] for i in range(12)]
def choices(xm: Board) -> Choices:
''' Given matrix of values, return matrix of choices. '''
c = lambda x: 255 if x == -1 else 1 << x
return [[c(xm[i][j]) for j in range(12)] for i in range(12)]Implementation of backtracking algorithm
We implement the backtracking algorithm as a function which we call solution. This function returns the first solution to the problem that is found, or None if no solution exists.
def solution(xm: Board) -> Optional[Board]:
''' Main function of backtracking algorithm. Given initial board xm,
compute filled board. Return None if no solution exists. '''
stack = [choices(xm)]
while stack:
cm = prune(stack.pop())
if reject(cm):
continue
if accept(cm):
return board(cm)
stack += expand(cm)
return NoneHere, we are using some functions which we will have to implement.
reject(cm: Choices) -> boolreturnsTruewhen we know that a partial candidate is no longer worth pursuing (because some of the constraints are not being satisfied).accept(cm: Choices) -> boolreturnsTruewhen the board is completely filled.expand(cm: Choices) -> list[Choices]chooses a cell with the lowest number of choices and returns a list of copies ofcm, but with the chosen cell replaced by each possible value.prune(cm: Choices) -> Choicesuses the constraints of the problem to rule out possibilities in each cell.
Of these, only the prune function has a lengthy implementation, so we leave that one for the next section.
We should reject a candidate if there is a cell such that no number in $\{0,\ldots,7\}$ could be in that cell or if the current board cannot be filled in such a way that we obtain a connected board. Notice that every constraint (except connectedness) will be enforced in the prune function, which will be implemented such that if a constraint is not met, then some cell will have zero choices available (in this case, we say that the cell is blocked).
def reject(cm: Choices) -> bool:
''' True iff a partially filled board will never lead to a sol. '''
return blocked(cm) or not connected(cm)
def blocked(cm: Choices) -> bool:
''' True iff there is a cell s.t. no 0 <= x <= 7 is in the cell. '''
return any(cm[i][j] == 0 for i, j in product(range(12), repeat=2))
def connected(cm: Choices) -> bool:
''' True iff there is a chance the partially filled board will lead
to a connected board. '''
mat = [[int(cm[i][j] != 1) for j in range(12)] for i in range(12)]
_, num_components = label(mat) # from scipy.ndimage import label
return num_components <= 1We accept a candidate if the board is completely filled. Notice that if accept is called in the solution function, since the candidate was not rejected, we know that every constraint is satisfied.
def accept(cm: Choices) -> bool:
''' True iff the board is completely filled. '''
return all(count[cm[i][j]] == 1 for i, j in product(range(12), repeat=2))The expand function can be implemented as follows.
def expand(cm: Choices) -> list[Choices]:
''' Given a partially filled board, choose the cell with lowest num
of possible values. Return list of copies of the board, where in the
cell, we replace by each possible value. '''
# find (a, b) such that count[cm[a][b]] is minimal
a, b = 0, 0
m = count[cm[a][b]]
for i, j in product(range(12), repeat=2):
if m <= 1 or (1 < count[cm[i][j]] < m):
a, b = i, j
m = count[cm[a][b]]
if m == 2:
break
# return list of copies of cm, but replacing cm[a][b] by each value
ans = []
for x in range(8):
if cm[a][b] & (1 << x):
cm_new = deepcopy(cm)
cm_new[a][b] = 1 << x
ans.append(cm_new)
return ansImplementation of the prune function
The prune function has the following structure.
def prune(cm: Choices) -> Choices:
''' Given partially filled board, use constraints of the problem to
remove numbers from the list of possibilities of each cell. '''
ans = deepcopy(cm)
# prune based on: every 2x2 square must have at least one 0
# ...
# prune based on: each subgrid has one 1, ..., seven 7
# ...
# prune based on: each subgrid row/col has 4 numbers, sum = 20
# ...
# prune based on: each row/col has a sum given by the large blue numbers
# ...
# prune based on: 'line of sight' of the small blue numbers
# ...
return ansAt every step, we update the matrix ans. Here is how each pruning step can be implemented.
Every $2 \times 2$ square should have at least one $0$:
for i, j in product(range(11), repeat=2):
for corner in range(4):
a = i + ((corner + 1) % 4 > 1)
b = j + (corner > 1)
# if all cells except (a, b) do not have a 0,
# then cell (a, b) can't be > 0.
remove = True
for corner_ in range(4):
if corner_ != corner:
a_ = i + ((corner_ + 1) % 4 > 1)
b_ = j + (corner_ > 1)
remove &= not (ans[a_][b_] & 1)
if remove:
ans[a][b] &= 1Each subgrid has one $1$, …, seven $7$’s:
for grid in range(4):
i0 = 5 if ((grid + 1) % 4 > 1) else 0
i1 = 12 if ((grid + 1) % 4 > 1) else 7
j0 = 5 if grid % 4 > 1 else 0
j1 = 12 if grid % 4 > 1 else 7
coordinates = {x: [] for x in range(8)}
for i, j in product(range(i0, i1), range(j0, j1)):
if count[ans[i][j]] == 1:
coordinates[value[ans[i][j]]].append((i, j))
for x in range(1, 8):
# If there are x or more cells with only possibility x,
# x is not in the other cells
if len(coordinates[x]) >= x:
for i, j in product(range(i0, i1), range(j0, j1)):
if (i, j) not in coordinates[x][:x]:
ans[i][j] &= (1 << x) ^ 255Each row/column in a subgrid has $4$ positive numbers which sum to $20$:
for grid in range(4):
i0 = 5 if ((grid + 1) % 4 > 1) else 0
i1 = 12 if ((grid + 1) % 4 > 1) else 7
j0 = 5 if grid % 4 > 1 else 0
j1 = 12 if grid % 4 > 1 else 7
rows = [[(i, j) for j in range(j0, j1)] for i in range(i0, i1)]
cols = [[(i, j) for i in range(i0, i1)] for j in range(j0, j1)]
arrs = rows + cols
for arr in arrs:
cms = [ans[i][j] for (i, j) in arr]
num_zeros = sum(value[c] == 0 for c in cms if count[c] == 1)
num_posit = sum(value[c] >= 1 for c in cms if count[c] == 1)
n = 4 - num_posit
s = 20 - sum(value[c] for c in cms if count[c] == 1)
if not (num_zeros <= 3 and num_posit <= 4) or (n == 0 and s != 0):
return [[0 for _ in range(12)] for _ in range(12)]
# loop over unknown cells
for (i, j), c in zip(arr, cms):
if count[c] > 1:
# loop over x s.t. x is not part of partition
for x in range(1, 8):
if n and not (n - 1 <= s - x <= 7*(n - 1)):
ans[i][j] &= (1 << x) ^ 255Each row/column has a sum given by the large blue numbers:
rows = [(blue[0][i], [(i, j) for j in range(5, 7)]) for i in range(12)]
cols = [(blue[3][j], [(i, j) for i in range(5, 7)]) for j in range(12)]
arrs = rows + cols
for bluenum, arr in arrs:
if bluenum <= 7:
continue
cms = [ans[i][j] for (i, j) in arr]
n = sum(count[c] != 1 for c in cms)
s = 40 - bluenum - sum(value[c] for c in cms if count[c] == 1)
if n == 0 and s != 0:
return [[0 for _ in range(12)] for _ in range(12)]
# loop over unknown cells
for (i, j), c in zip(arr, cms):
if count[c] > 1:
# loop over x s.t. x is not part of partition
for x in range(1, 8):
if n and not (0 <= s - x <= 7*(n - 1)):
ans[i][j] &= (1 << x) ^ 255A small blue number indicates the first number seen in that direction:
for side, a in product(range(4), range(12)):
bluenum = blue[side][a]
if 1 <= bluenum <= 7:
for b in range(12):
i = a if not side % 2 else (b if side == 3 else 11 - b)
j = a if side % 2 else (b if not side else 11 - b)
if ans[i][j] != 1:
# remove all except {0, bluenum} from ans[i][j]
for x in range(1, 8):
if x != bluenum:
ans[i][j] &= (1 << x) ^ 255
breakSolution
We now have the solution function fully implemented. We compute the solution to the problem with the following line of code:
sol = solution(matrix)Here, matrix is a Board containing the initial grid we were given. This program solves the problem in approximately $1.5$ seconds (on my machine), and we obtain the following filled grid:
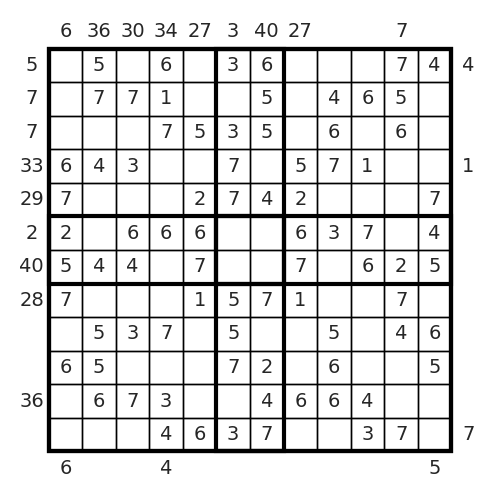
Therefore, the product of the areas of the connected groups of squares with a $0$ is
\[9 \times 8 \times 6 \times 6 \times 5 \times 5 \times 4 \times 4 \times 4 \times 3 \times 3 \times 2 \times 1 \times 1 \times 1 \times 1 \times 1 = 74649600.\]